Al final del número de la semana pasada mencioné que la mayor parte de las estrategias que existen para lidiar con NAs pueden ser agrupadas en cuatro grandes categorías:
- Omitir temporalmente observaciones con valores faltantes
- Eliminar permanentemente renglones o columnas con uno o más NAs
- Reemplazar NAs por otro valor (0s, el promedio de la variable, etc.)
- Obtener más información
En esta entrega exploro las primeras dos y la próxima semana concluiré esta guía cubriendo las dos restantes (lo sé, lo sé, mi plan era terminar esta semana, pero... ¡hay tanto que decir!).
Antes de arrancar, quiero enfatizar tres puntos.
Primero, todos los métodos que existen para trabajar con valores faltantes tienen ventajas, desventajas y son falibles. Debes usarlos con conocimiento de causa y precaución.
Segundo, el uso de estos métodos está condicionado en buena medida por la naturaleza del tipo de valores faltantes que tienes enfrente (por eso me clavé tanto en el tema la semana pasada).
Tercero, sea cual sea el método que elijas, es una buena práctica que se lo comuniques explícita y transparentemente a tu audiencia. Esto le permitirá estar al tanto del reto que enfrentaste, así como tener elementos para valorar tus decisiones.
A darle.
Hace un par de semanas, al iniciar esta guía básica, mencioné que los valores faltantes son contagiosos en R.
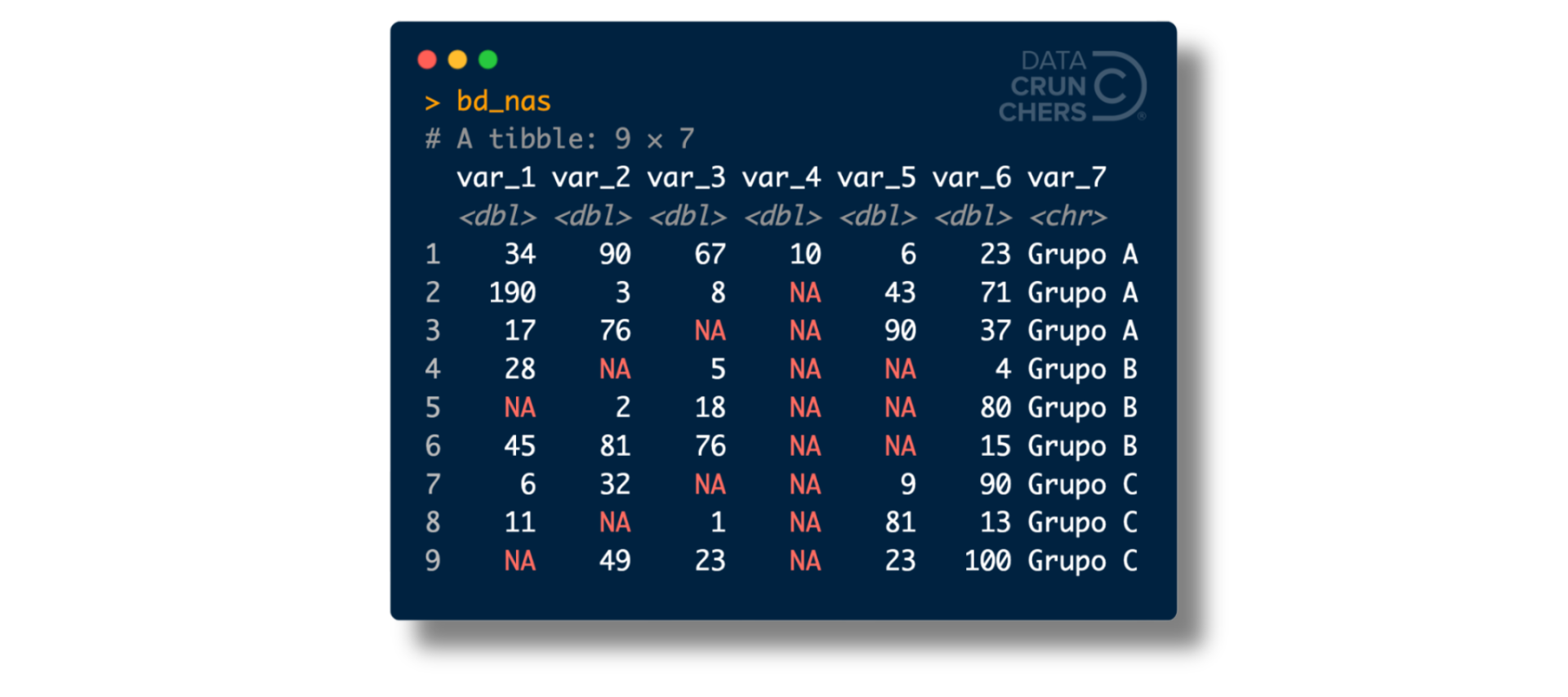
Para entender mejor a qué me refiero, utilizaré la siguiente mini base de datos:
Puedes construirla con los siguientes bloques de código:
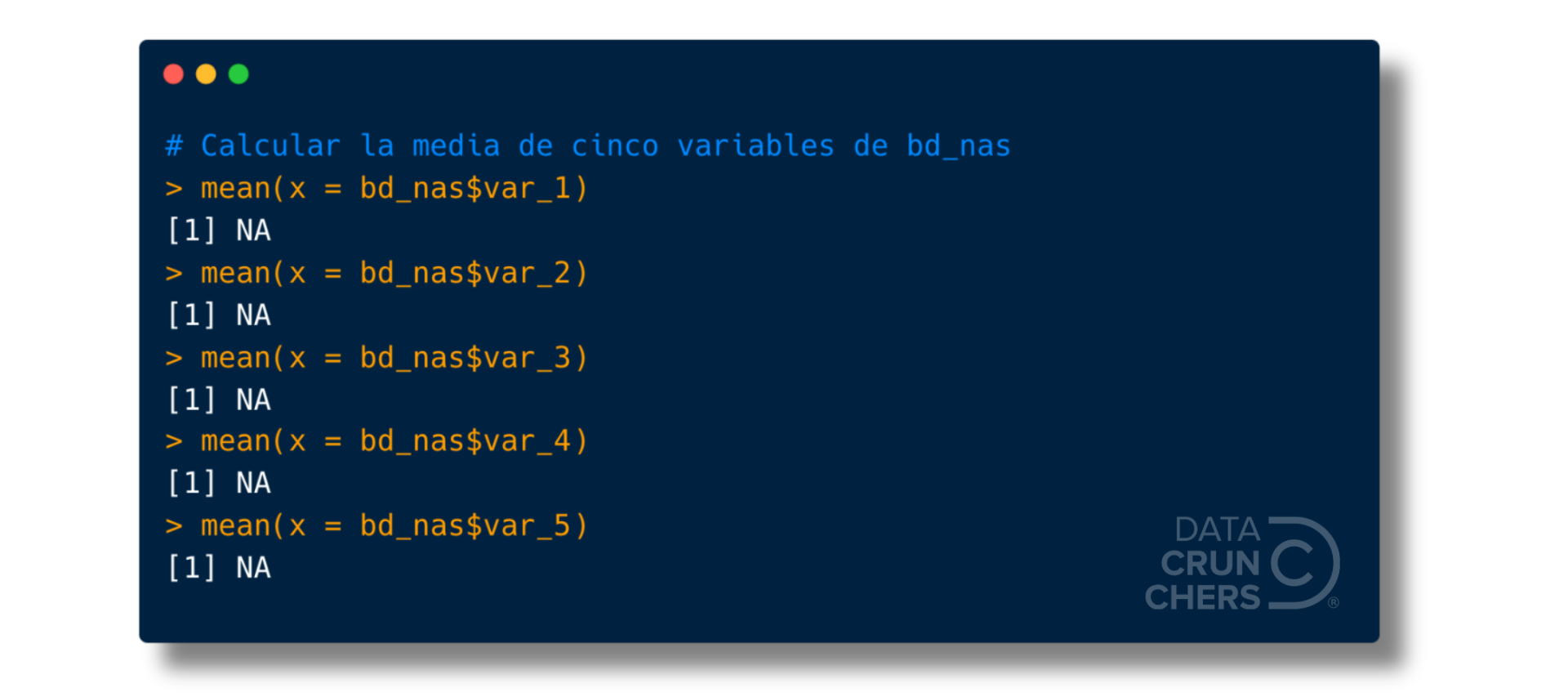
Si después de construir el objeto bd_nas intentas calcular la media de cualquiera de sus primeras cinco variables usando la función mean(), obtendrás como resultado el valor NA.
Puedes confirmarlo copiando y ejecutando las siguientes líneas de código:
Si lo haces, deberías ver algo como esto en tu consola:
Esto no se debe ni se limita a la función mean().
Puedes comprobarlo copiando y ejecutando estos otros ejemplos de código:
En todo los casos, el "problema" radica en que R encuentra al menos un valor faltante en la o las columnas que le indicamos que usara, y como no sabe cuál es su verdadero valor, entonces concluye que el resultado debe ser NA.
Dada lo común que es este "problema", todas las funciones que usé hasta ahora, y varias más que enlisto en los recursos de esta semana, incluyen un argumento para indicarle a R que deseamos omitir los valores faltantes...
En el caso de mean(), tenemos que modificar el valor del argumento na.rm para que sea TRUE en lugar de FALSE (el default).
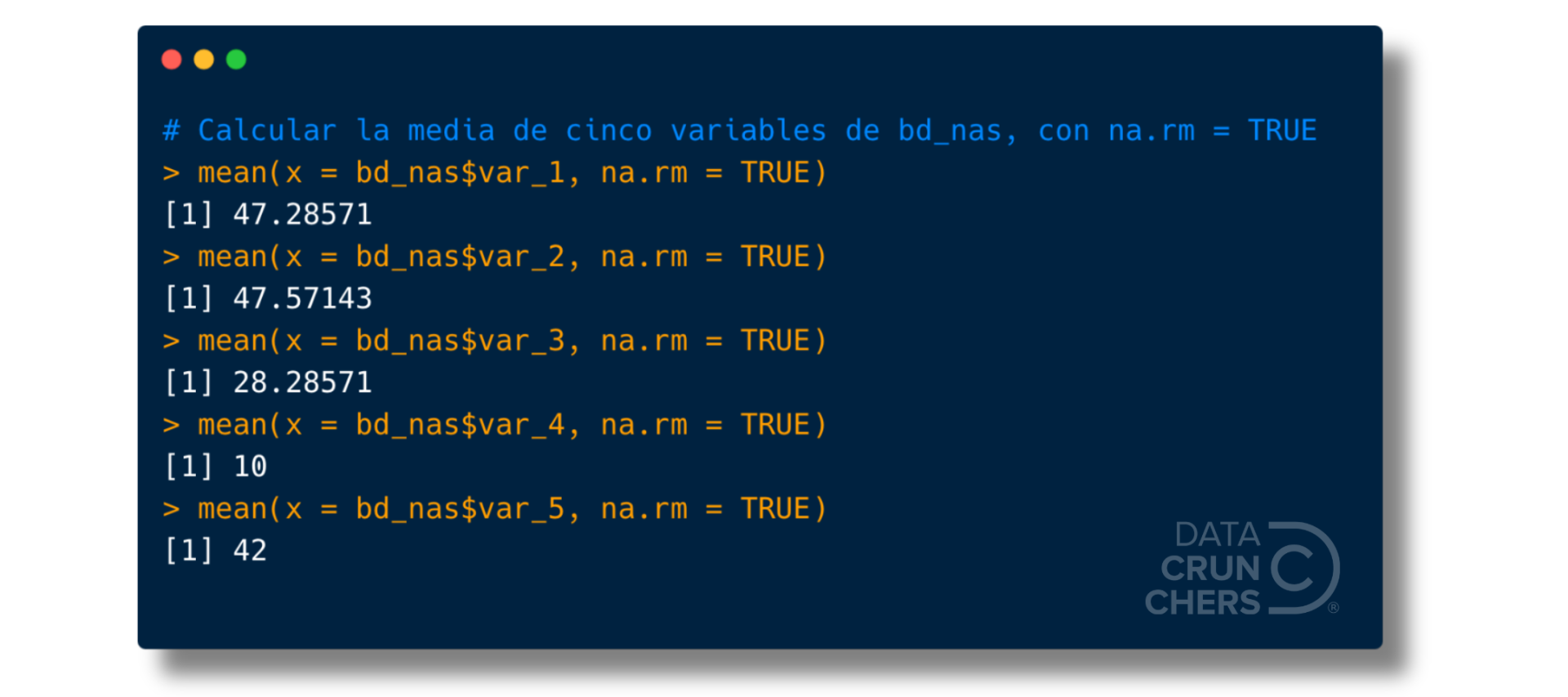
Los siguientes chunks de código ilustran cómo hacerlo:
Si los copias, pegas y ejecutas, verás los siguientes resultados:
En términos formales, esta solución se conoce como eliminación por pares o pairwise deletion y consiste en calcular lo que te interesa (p. ej., la media, varianza o coeficiente de correlación) usando únicamente los valores que sí están disponibles.
El siguiente bloque ofrece otros ejemplos de código de funciones que ofrecen la opción de pairwise deletion:
Esta solución es sencilla y práctica, pero tiene al menos dos riesgos.
Primero, puede generarnos una falsa sensación de que "resolvimos" el problema.
Para entender mejor por qué, echa un ojo a var_4 en el tibble bd_nas:
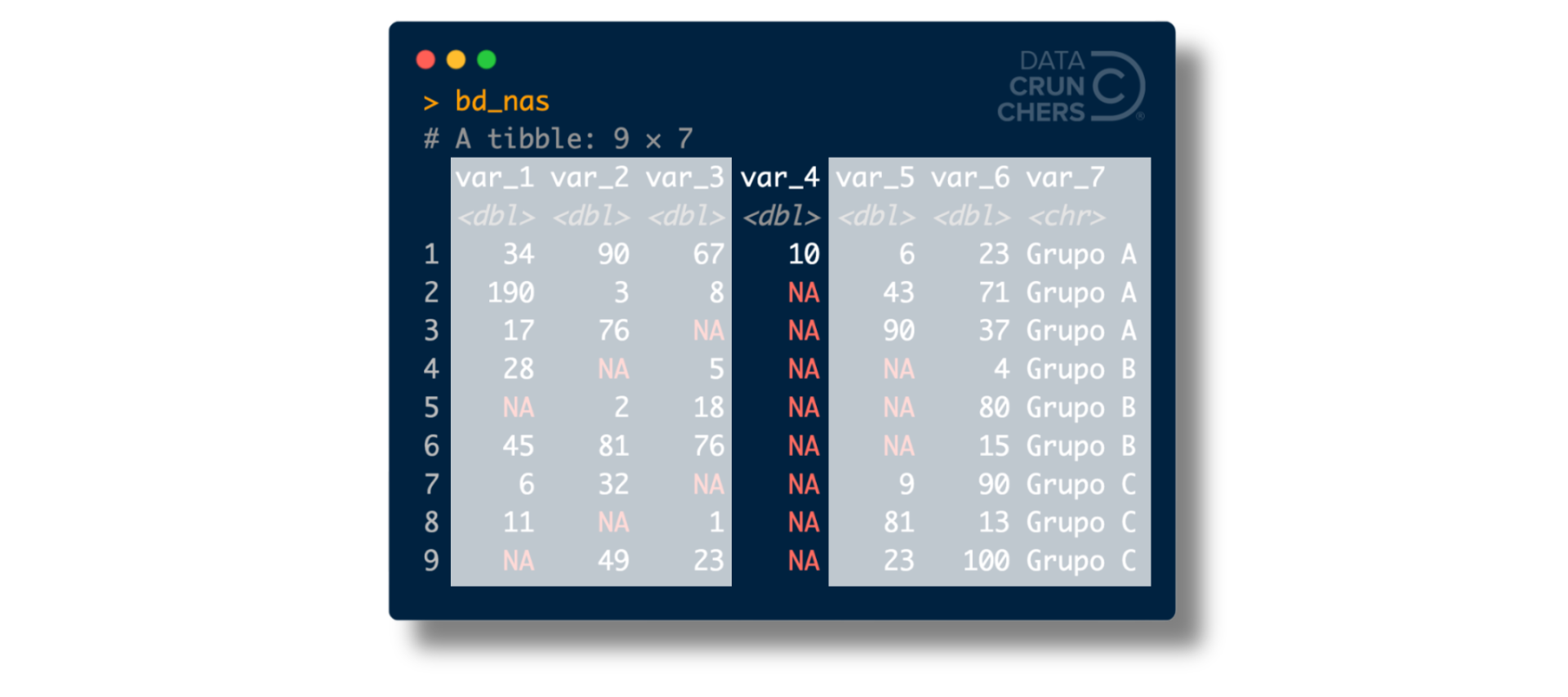
Si calculamos su media usando na.rm = TRUE obtendremos como resultado el número 10.
¡Pero ocho de los nueve valores de esta variable son faltantes!
¿De qué nos sirve calcular la media de una variable a partir de un solo valor?
El problema está lejos de ser "resuelto".
Y si bien construí esta variable para ilustrar un caso extremo, esto nos lleva a un terreno complicado: ¿qué tanto es tantito?
Es decir, ¿a partir de qué porcentaje de valores faltantes en una variable debemos preocuparnos al usar na.rm = TRUE o equivalentes?
De acuerdo con Little y Rubin, no hay una regla clara, pues la decisión no sólo depende del porcentaje de valores faltantes, sino también de su naturaleza.
Ya sé... No es lo que esperabas leer.
El segundo riesgo potencial de usar la eliminación por pares es que no siempre es adecuada.
Concentrémonos en la var_5 del tibble bd_nas:
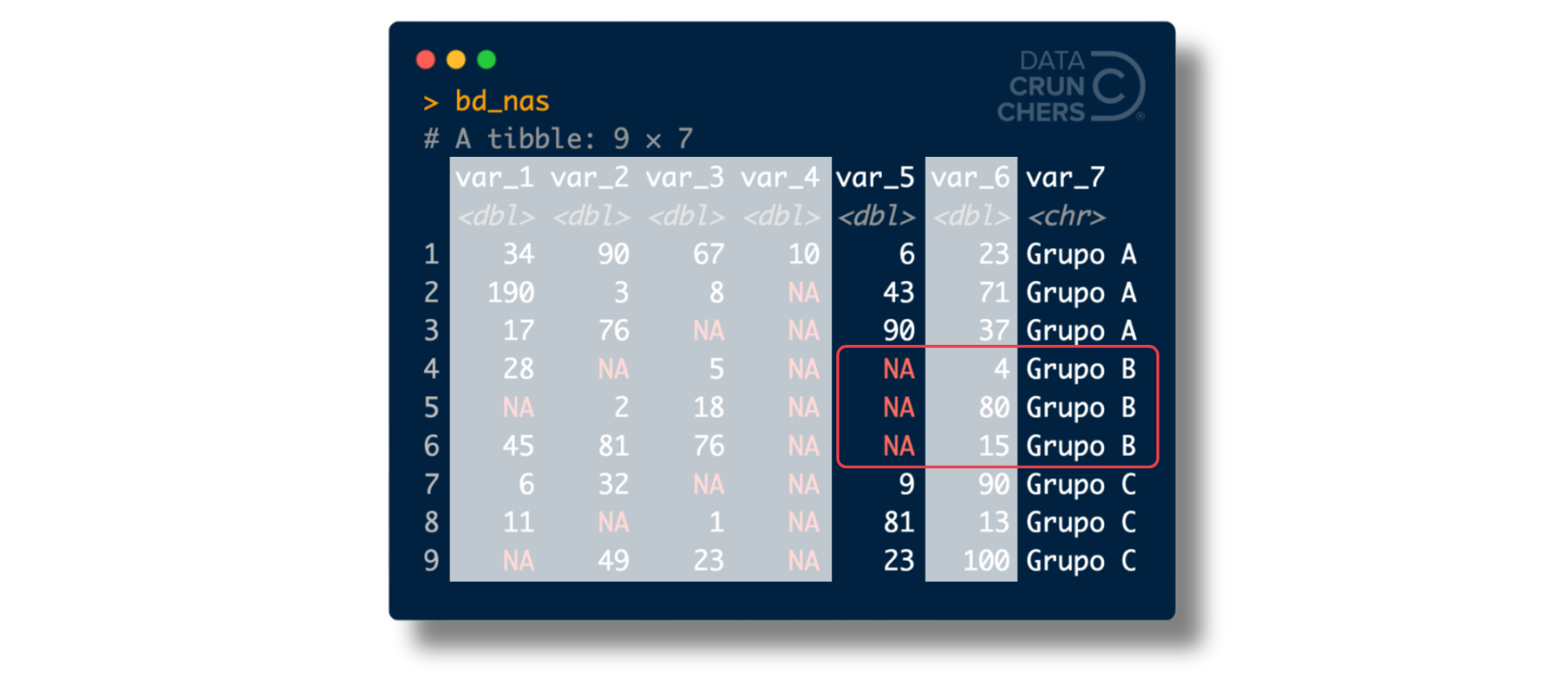
Ésta tiene tres valores faltantes, cifra parecida a las dos en var_1, var_2 y var_3.
Sin embargo, hay una diferencia importante.
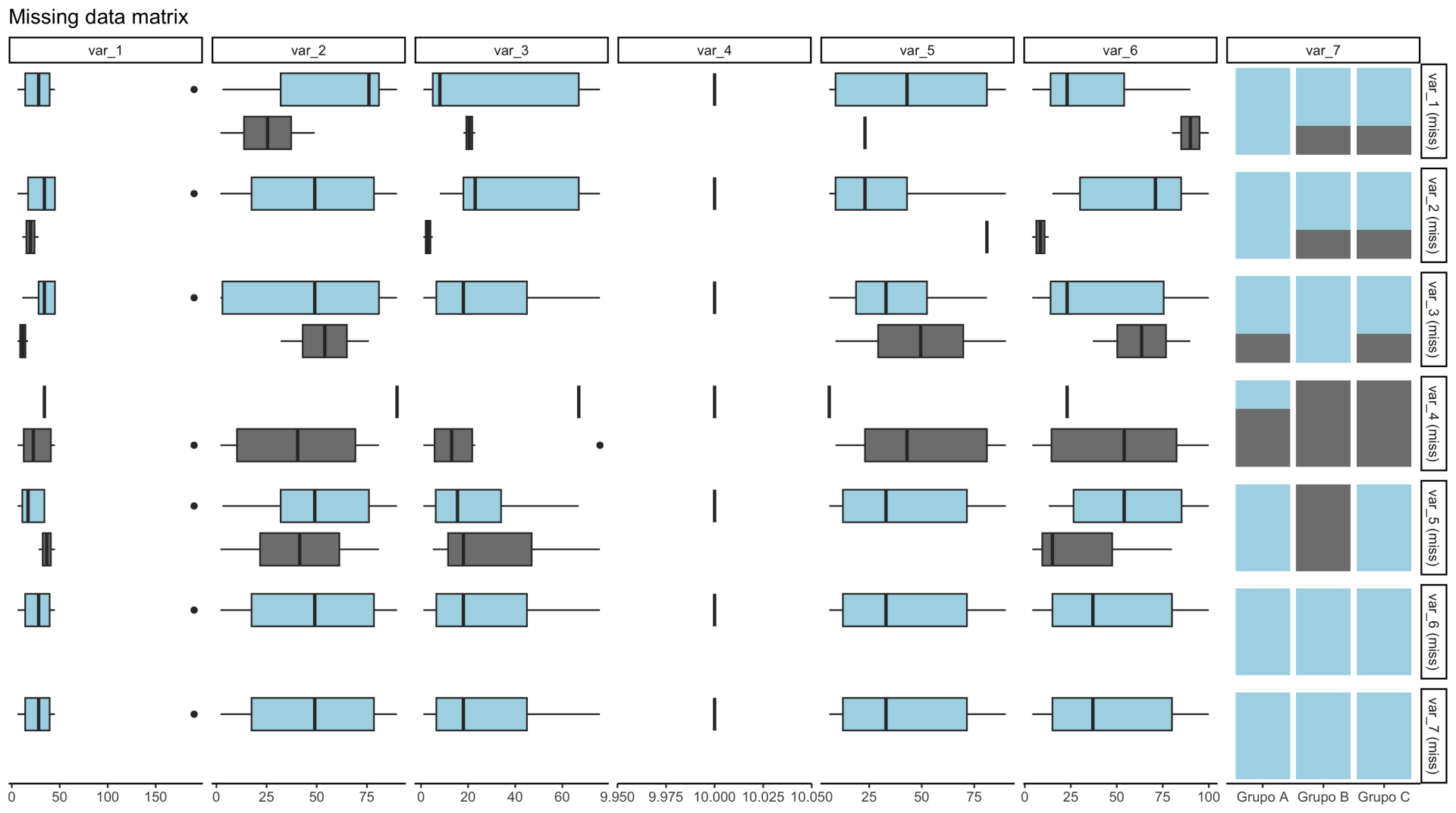
Como ilustra el recuadro rojo en la imagen de arriba, los tres valores faltantes de var_5 están correlacionados con el valor Grupo B de la var_7, lo que sugiere al menos dos cosas:
Esto último puede introducir un sesgo importante en nuestras estimaciones 😒.
La próxima semana incluiré algunas recomendaciones respecto al tipo de solución que es recomendable dada la naturaleza de los valores faltantes.
Por ahora te adelanto que la eliminación por pares es una alternativa adecuada si los valores faltantes en tu base de datos son completamente aleatorios... cosa que, como comenté la semana pasada, no es muy común.
El segundo conjunto de alternativas para lidiar con NAs es más drástico (y potencialmente costoso) que omitir temporalmente los valores faltantes de una o más variables.
Implica eliminar por completo y de forma permanente, los renglones que contienen al menos un valor faltante.
Esta solución suele llamarse eliminación por lista o listwise deletion.
Mientras que ésta es la solución que adoptan por default otros programas (les estoy hablando a ustedes, SPSS y Stata) cuando se topan con uno o más NAs en un renglón, en R tenemos que implementarla explícitamente en la mayoría de las ocasiones.
Partiendo del tibble bd_nas, los siguientes bloques de código ofrecen dos opciones para eliminar todos los renglones con al menos un NA:
Si ejecutas cualquiera de estas líneas obtendrás el siguiente resultado:
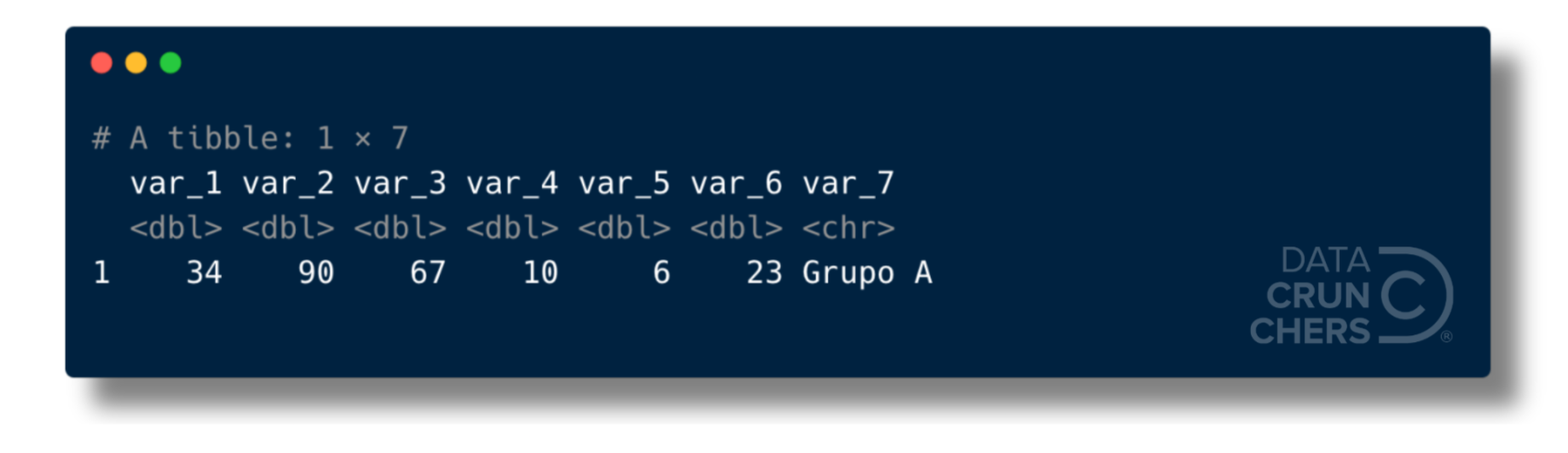
Pasamos de un tibble con nueve observaciones a otro con un sólo renglón 🤯.
Cierto, diseñé el tibble bd_nas para que al llegar a este punto viéramos un ejemplo extremo de lo que puede ocurrir si usamos la eliminación por lista de renglones.
Pero este resultado es útil para ilustrar al menos tres desventajas de usar esta alternativa:- Trata a todos los renglones de la misma forma, sin importar si contienen uno, cinco o 10 valores faltantes;
- Si la base de datos registra información de períodos consecutivos de tiempo, eliminar uno o más de sus renglones provocará que se interrumpa la serie; y,
- Es probable que en el proceso perdamos muchas observaciones (en este famoso paper, King & Co. sugieren que la cifra puede oscilar entre 30% y 90%)
Detengámonos un momento en esto último. ¿Cuáles podrían ser las implicaciones?
Si calculamos la media de var_1 con la versión original de bd_nas omitiendo temporalmente los valores faltantes, R usará siete observaciones (78% del total) y arrojará el valor 47.28571.
Pero si lo hacemos con la versión de bd_nas que obtenemos después de eliminar todos los renglones con al menos un valor faltante, R sólo tendrá una observación para trabajar (11% del total) y el valor de la misma, 34, será el de la media.
Puedes comprobando ejecutando los siguientes bloques de código:
En este caso en particular, la eliminación por lista de renglones provoca que perdamos mucha información valiosa que sí tenemos y deberíamos aprovechar.
Este problema se mitiga al trabajar con bases de datos más grandes.
Pero incluso si nuestra base original tuviera 1 millón de observaciones y después de eliminar los renglones con NAs nos quedamos con la mitad, si la naturaleza de los valores faltantes no es completamente aleatoria, la eliminación por lista puede sesgar las estimaciones que hagamos con la información disponible.
Como probablemente estás pensando, así como podemos eliminar los renglones que contienen uno o más valores faltantes, podemos hacer lo mismo con las columnas.
A continuación encontrarás dos opciones para realizar este procedimiento:
Sin importar cuál uses, el tibble resultante se verá así:
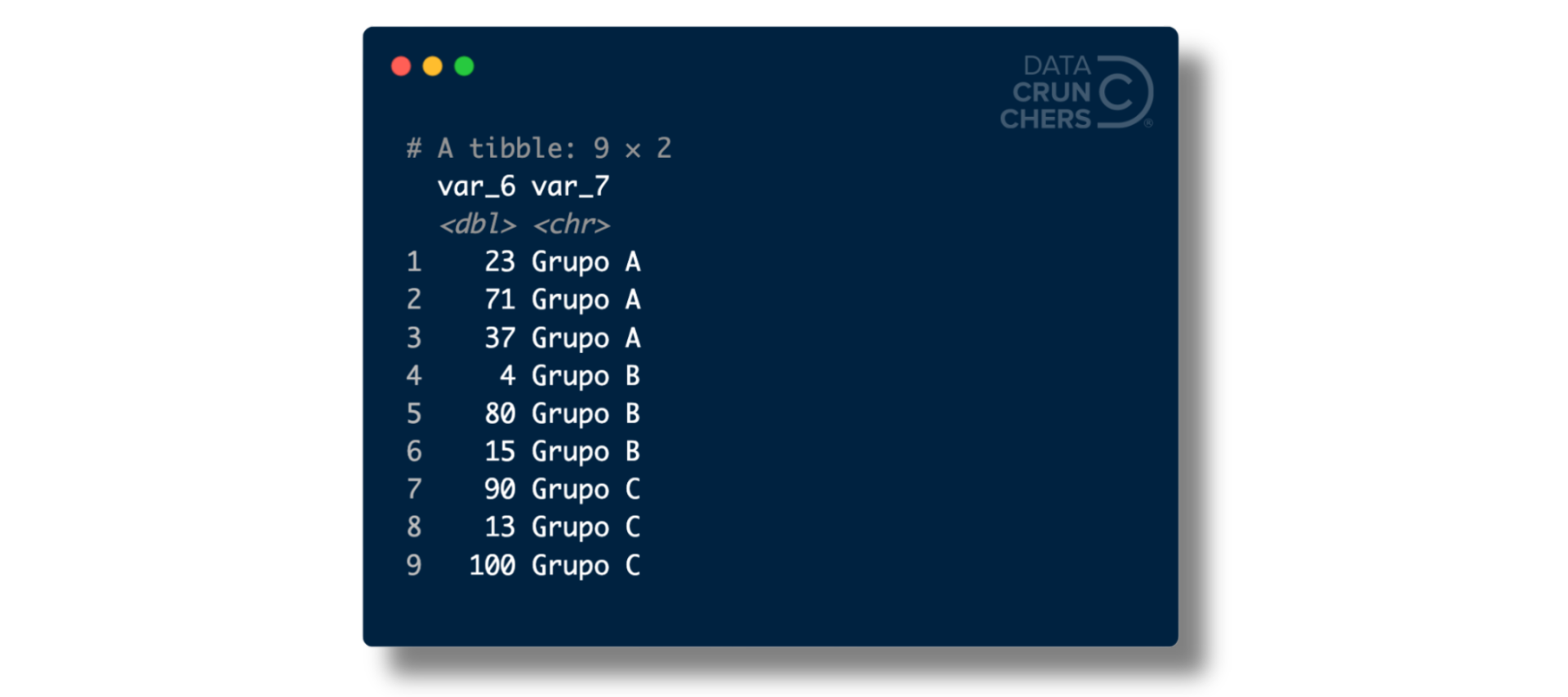
En este ejemplo pasamos de un tibble con siete columnas a uno de dos.
De nuevo, si bien es un caso extremo, ilustra que la primera y tercera desventajas que mencioné antes para la eliminación por lista de renglones, también podrían presentarse cuando usamos este método para las columnas.
Y a estos dos problemas, se suma uno más.
Las columnas representan variables.
Éstas suelen ser clasificadas como de respuesta (o dependientes) y explicativas (o independientes).
Si usamos este método para lidiar con los valores faltantes en nuestras columnas, y nuestra variable de respuesta (lo que queremos explicar) o nuestra principal variable explicativa contienen al menos un valor faltante, terminaríamos borrándolas.
Lo cual, por decir lo menos, es un resultado subóptimo 🫠.
-----
Si la omisión temporal de valores faltantes y la eliminación permanente de renglones y/o columnas presentan todas estas limitaciones y riesgos...
¿Qué hacemos entonces?
Mi punto no es que nunca debas optar por estas soluciones, sino que cuando la uses, lo hagas con precaución y pleno conocimiento de sus posibles implicaciones.
Y que si concluyes que estas alternativas no son adecuadas dada la naturaleza de tu análisis y los valores faltantes que tiene tu base de datos, explores si la solución radica en reemplazar los NAs por otros valores.
¿Juuuuat? 😮
La próxima semana te contaré de esta tercera familia de soluciones.
Por ahora, paso a los recursos de la semana.